Spiral series

1. Spiral with increasing density
2. Spiral with varying height
3. Shaded spiral
4. Sphere forming spiral
5. Textured spherical spiral
6. Textured and shaded spherical spiral

1. Spiral with increasing density

From every point in the spiral, subdivided line is traced. Line segments are connected between the neighbors. Line segment count progressively increases towards the center.

spiral.bas

DECLARE SUB DrawLine (startX AS DOUBLE, startY AS DOUBLE, endX AS DOUBLE, endY AS DOUBLE, col AS INTEGER)
' Program to render fancy looking spiral.
' By Svjatoslav Agejenko.
' Email: svjatoslav@svjatoslav.eu
' Homepage: http://www.svjatoslav.eu
'
' Changelog:
' 2003.12, Initial version
' 2024.08, Improved program readability using AI

DIM SHARED lineVertexX(1 TO 100) AS DOUBLE
DIM SHARED lineVertexY(1 TO 100) AS DOUBLE
DIM SHARED depth AS INTEGER
DIM SHARED tempDepth AS INTEGER
SCREEN 12

' Initialize the scale factor for the spiral
spiralScaleFactor = 200
depth = 0

' Generate the spiral by iterating through angles and scaling appropriately
FOR angle = 1 TO 30 STEP .1
    ' Calculate the current scale based on the remaining distance to the center
    spiralScaleFactor = (30 - angle) * 7
    ' Convert polar coordinates to cartesian for the current point
    xPosition = SIN(angle) * spiralScaleFactor + 200
    yPosition = COS(angle) * spiralScaleFactor + 200
    ' Store the current depth (z-axis value)
    tempDepth = angle
    ' Draw a line from the previous point to the current point with a color based on depth
    DrawLine xPosition + (xPosition / 2) + (angle * 3), (yPosition - (xPosition / 3)) + (angle * 3), xPosition + 25, yPosition + 25 - (angle * 3), depth
    ' Set the color for the next segment
    depth = 15
NEXT angle

' Wait for user input to close the program
userInput$ = INPUT$(1)

SUB DrawLine (startX AS DOUBLE, startY AS DOUBLE, endX AS DOUBLE, endY AS DOUBLE, col AS INTEGER)
    ' Calculate the step increments for x and y based on the depth
    deltaX = (endX - startX) / tempDepth
    deltaY = (endY - startY) / tempDepth

    FOR segmentIndex = 1 TO tempDepth
        ' If there is a previous vertex, draw a line to the new starting point
        IF lineVertexX(segmentIndex) > 0 THEN LINE (lineVertexX(segmentIndex), lineVertexY(segmentIndex))-(startX, startY), col
        ' Store the current starting point as the next vertex
        lineVertexX(segmentIndex) = startX
        lineVertexY(segmentIndex) = startY
        ' Increment the starting point by the calculated deltas
        startX = startX + deltaX
        startY = startY + deltaY
        ' Draw a line from the stored vertex to the new starting point
        LINE (lineVertexX(segmentIndex), lineVertexY(segmentIndex))-(startX, startY), col
    NEXT segmentIndex
END SUB

2. Spiral with varying height

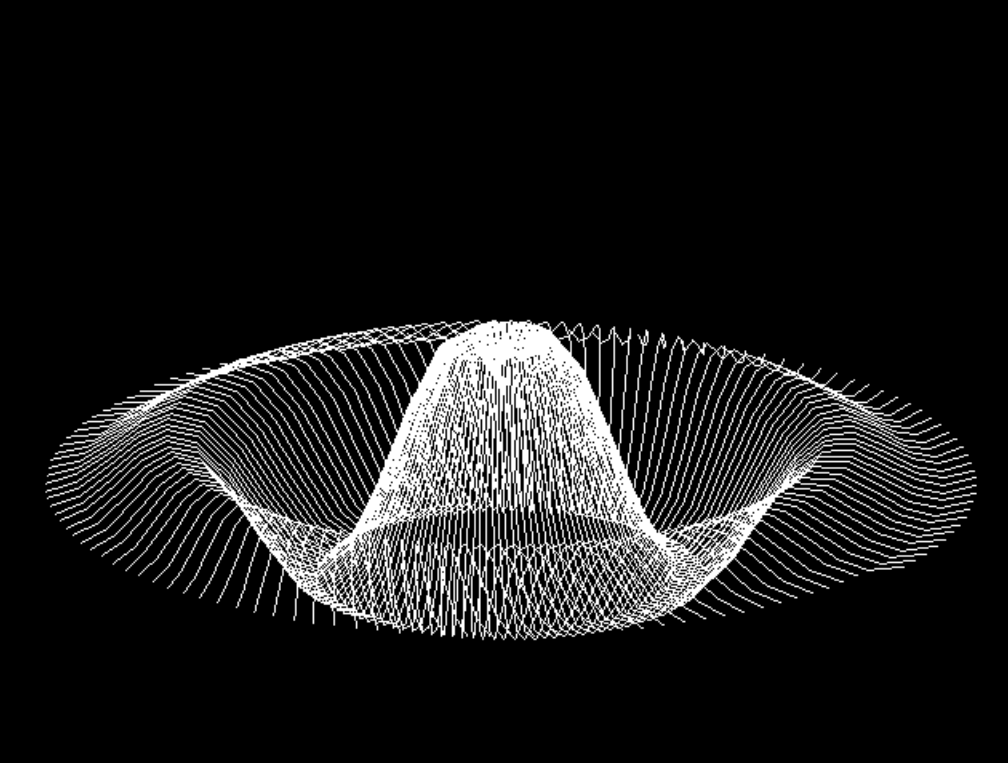
spiral, 2.png

From every point in the spiral, subdivided line is traced. Line segments are connected between the neighbors. This creates effect where lines run from edges towards the center. Center is vertically displaced by sinus function where input is the distance to the center.

spiral, 2.bas

' Program to render fancy looking spiral.
' By Svjatoslav Agejenko.
' Email: svjatoslav@svjatoslav.eu
' Homepage: http://www.svjatoslav.eu
'
' Changelog:
' 2003.12, Initial version
' 2024.08, Improved program readability using AI

DIM SHARED spiralX(1 TO 10000) AS SINGLE ' X coordinates of the spiral points
DIM SHARED spiralY(1 TO 10000) AS SINGLE ' Y coordinates of the spiral points
DIM SHARED pointCount AS INTEGER ' Total number of points plotted
SCREEN 12 ' Set screen resolution to 640x480 with 16 colors

' Initialize the scale factor for the spiral
scaleFactor = 200
pointCount = 0

' Calculate and plot each point on the spiral
FOR angle = 1 TO 100 STEP .05
    pointCount = pointCount + 1
    scaleFactor = 100 - angle ' Update the scaling factor as the loop progresses

    ' Calculate the X and Y coordinates based on the sine and cosine of the angle
    spiralX(pointCount) = SIN(angle) * scaleFactor * 3 + 320
    spiralY(pointCount) = COS(angle) * scaleFactor + 300

    ' Apply a vertical displacement to create a more dynamic effect
    spiralY(pointCount) = spiralY(pointCount) + (SIN((angle + 20) / 10) * angle)

    ' Plot the point on the screen
    PSET (spiralX(pointCount), spiralY(pointCount)), 15
NEXT angle

' Draw lines between points to create the spiral effect
FOR segmentStart = 1 TO pointCount - 125
    LINE (spiralX(segmentStart), spiralY(segmentStart)) - _
         (spiralX(segmentStart + 125), spiralY(segmentStart + 125)), 15
NEXT segmentStart

' Wait for user input before exiting
a$ = INPUT$(1)
END ' Exit the program

3. Shaded spiral

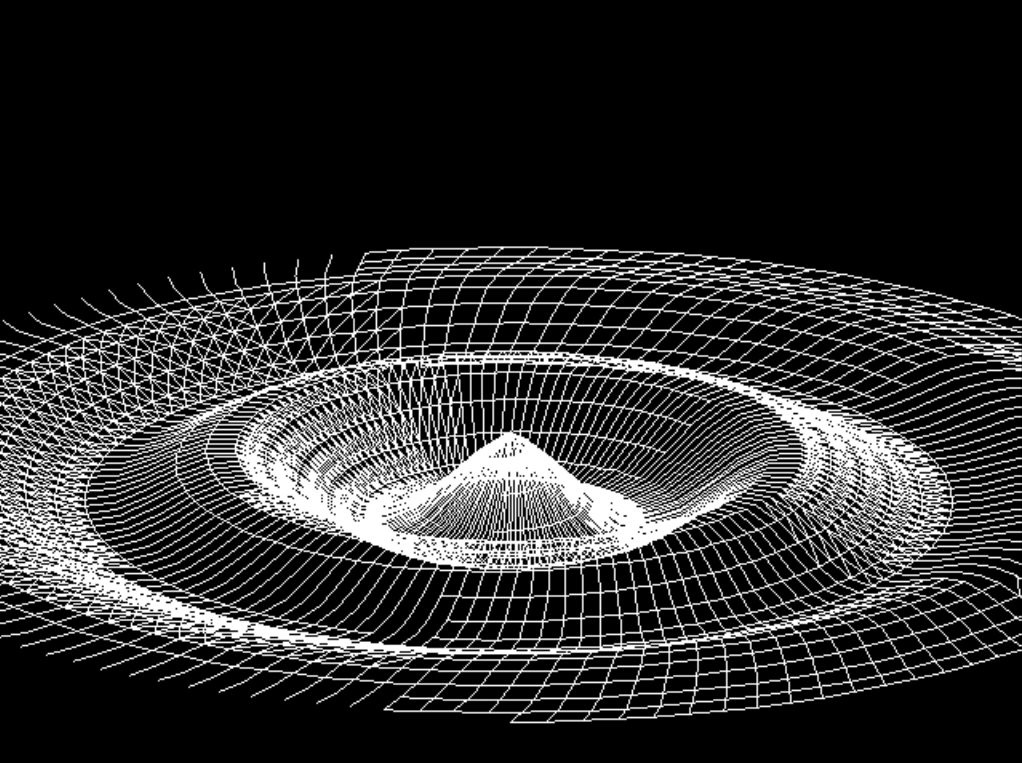
spiral, 3.png

Similar to previous spiral, Line segments are connected between the neighbors and sinus from the center decides vertical displacement. Attempt of shading is made where brighter areas have more detail.

spiral, 3.bas

' Program to render fancy looking spiral with shaded surface.
' By Svjatoslav Agejenko.
' Email: svjatoslav@svjatoslav.eu
' Homepage: http://www.svjatoslav.eu
'
' Changelog:
' 2003.12, Initial version
' 2024.08, Improved program readability using AI

' Declare shared arrays for storing coordinates and sine values
DIM SHARED spiralX(1 TO 10000)
DIM SHARED spiralY(1 TO 10000)
DIM SHARED sineValue1(1 TO 10000)
DIM SHARED sineValue2(1 TO 10000)


' Set the screen mode to 640x480 with 16 colors
SCREEN 12

' Initialize the spiral rotation parameter
DIM spiralRotation AS SINGLE
spiralRotation = 0

' Generate and draw the spiral points
FOR angle = 0 TO 150 STEP .05
    spiralRotation = spiralRotation + 1
    scaleFactor = 150 - angle

    ' Calculate the X and Y coordinates for the current point
    spiralX(spiralRotation) = SIN(angle) * scaleFactor * 3 + 320
    spiralY(spiralRotation) = COS(angle) * scaleFactor + 300

    ' Apply additional vertical displacement based on a secondary sine function
    spiralY(spiralRotation) = spiralY(spiralRotation) + (SIN((angle + 20) / 10) * (angle / 5 + 1))

    ' Store the current sine values for later use
    sineValue1(spiralRotation) = SIN(angle)
    sineValue2(spiralRotation) = SIN((angle + 20) / 10)

    ' Draw the current point on the screen
    PSET (spiralX(spiralRotation), spiralY(spiralRotation)), 15
NEXT angle

' Connect the points to form a continuous line
FOR index = 1 TO spiralRotation - 127
    ' Draw a line segment between points 126 steps apart
    LINE (spiralX(index), spiralY(index))-(spiralX(index + 126), spiralY(index + 126)), 15

    ' Initialize the line drawing flag
    DIM drawLine AS INTEGER
    drawLine = 1

    ' Check conditions to determine if a line segment should be drawn
    IF sineValue1(index) > .8 AND sineValue2(index) < sineValue2(index + 125) THEN drawLine = 0
    IF sineValue1(index) < -.2 AND (sineValue2(index) - .4) > sineValue2(index + 125) THEN drawLine = 0

    ' Draw a line segment if the conditions are met
    IF drawLine = 1 THEN LINE (spiralX(index), spiralY(index))-(spiralX(index + 1), spiralY(index + 1)), 15

    ' Reset the line drawing flag and check for different conditions
    drawLine = 0
    IF sineValue1(index) > .8 AND sineValue2(index) > sineValue2(index + 125) THEN drawLine = 1
    IF sineValue1(index) < -.2 AND sineValue2(index) < sineValue2(index + 125) THEN drawLine = 1

    ' Draw a line segment if the conditions are met
    IF drawLine = 1 THEN LINE (spiralX(index), spiralY(index))-(spiralX(index + 127), spiralY(index + 127)), 15

    ' Reset the line drawing flag and check for another set of conditions
    drawLine = 0
    IF sineValue1(index) > .9 AND sineValue2(index) > sineValue2(index + 125) THEN drawLine = 1
    IF sineValue1(index) < -.5 AND sineValue2(index) < sineValue2(index + 125) THEN drawLine = 1

    ' Draw a line segment if the conditions are met
    IF drawLine = 1 THEN LINE (spiralX(index), spiralY(index))-(spiralX(index + 125), spiralY(index + 125)), 15
NEXT index

' Wait for a key press before exiting
a$ = INPUT$(1)

4. Sphere forming spiral

Similar to previous spiral, Line segments are connected between the neighbors. Spiral height and width are calculated such that they form multiple linked spherical shapes. Initially point cloud in shown:

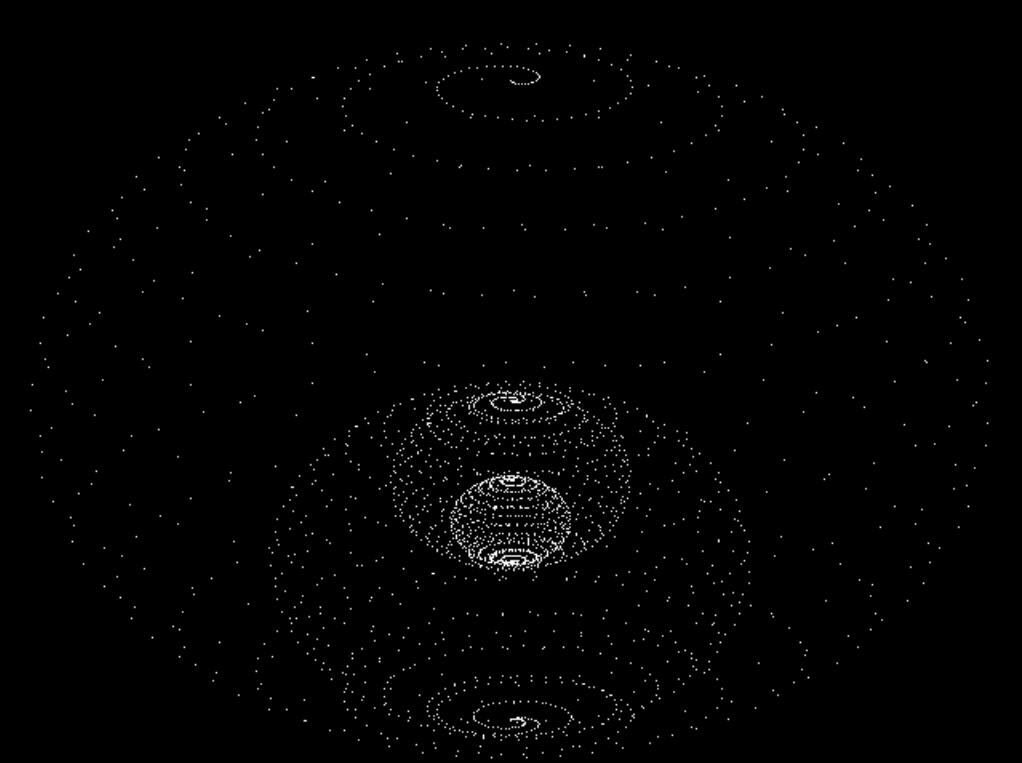
spiral, 4, 1.png

In the next step, points are connected using lines:

spiral, 4, 2.png

spiral, 4.bas

' Program to render fancy looking spiral.
' By Svjatoslav Agejenko.
' Email: svjatoslav@svjatoslav.eu
' Homepage: http://www.svjatoslav.eu
'
' Changelog:
' 2003.12, Initial version
' 2024.08, Improved program readability using AI

' Declare shared arrays to hold the x and y coordinates of the spiral
DIM SHARED spiralX(1 TO 10000)
DIM SHARED spiralY(1 TO 10000)

' Initialize the screen to a graphics mode with 640x480 resolution and 16 colors
SCREEN 12

' Constants for the initial size and the starting value of the index
CONST InitialSize = 100
CONST StartIndex = 0

' Variable to keep track of the current position in the spiral arrays
DIM torusIndex AS DOUBLE
torusIndex = StartIndex

' Loop parameters
DIM angle AS DOUBLE
DIM scaleFactor AS DOUBLE

' Generate the first arm of the spiral
FOR angle = 0 TO 97.35 STEP .15
    torusIndex = torusIndex + 1
    scaleFactor = SIN(angle / 31) * InitialSize
    spiralX(torusIndex) = SIN(angle) * scaleFactor * 3 + 320
    spiralY(torusIndex) = COS(angle) * scaleFactor + 250
    spiralY(torusIndex) = spiralY(torusIndex) - (COS(angle / 31) * 200)
    PSET (spiralX(torusIndex), spiralY(torusIndex)), 15
NEXT angle

' Generate the second arm of the spiral
FOR angle = 97.35 TO 0 STEP -.15
    torusIndex = torusIndex + 1
    scaleFactor = SIN(angle / 31) * (InitialSize / 2)
    spiralX(torusIndex) = SIN(angle) * scaleFactor * 3 + 320
    spiralY(torusIndex) = COS(angle) * scaleFactor + 350
    spiralY(torusIndex) = spiralY(torusIndex) - (COS(angle / 31) * 100)
    PSET (spiralX(torusIndex), spiralY(torusIndex)), 15
NEXT angle

' Generate the third arm of the spiral
FOR angle = 0 TO 97.35 STEP .15
    torusIndex = torusIndex + 1
    scaleFactor = SIN(angle / 31) * (InitialSize / 4)
    spiralX(torusIndex) = SIN(angle) * scaleFactor * 3 + 320
    spiralY(torusIndex) = COS(angle) * scaleFactor + 300
    spiralY(torusIndex) = spiralY(torusIndex) - (COS(angle / 31) * 50)
    PSET (spiralX(torusIndex), spiralY(torusIndex)), 15
NEXT angle

' Generate the fourth arm of the spiral
FOR angle = 97.35 TO 0 STEP -.15
    torusIndex = torusIndex + 1
    scaleFactor = SIN(angle / 31) * (InitialSize / 8)
    spiralX(torusIndex) = SIN(angle) * scaleFactor * 3 + 320
    spiralY(torusIndex) = COS(angle) * scaleFactor + 325
    spiralY(torusIndex) = spiralY(torusIndex) - (COS(angle / 31) * 25)
    PSET (spiralX(torusIndex), spiralY(torusIndex)), 15
NEXT angle

' Calculate the number of lines to draw based on the current index
DIM totalSegments AS DOUBLE
totalSegments = (torusIndex - 42) / 4

a$ = INPUT$(1)
' Clear the screen before drawing the lines
CLS

' Draw the lines between points in the spiral
FOR angle = 1 TO totalSegments * 4
    LINE (spiralX(angle), spiralY(angle))-(spiralX(angle + 42), spiralY(angle + 42)), 15
    LINE (spiralX(angle), spiralY(angle))-(spiralX(angle + 1), spiralY(angle + 1)), 15
NEXT angle

' Wait for the user to press a key before exiting
a$ = INPUT$(1)

' End of program
SYSTEM

5. Textured spherical spiral

spiral, 5.png

Similar to previous spiral, Line segments are connected between the neighbors. Spiral height and width are calculated such that sphere is formed. Sphere is textured. Texture is loaded from file: texture.dat .Invisible surface detection and removal is attempted.

spiral, 5.bas

' Program to render fancy looking spiral.
' By Svjatoslav Agejenko.
' Email: svjatoslav@svjatoslav.eu
' Homepage: http://www.svjatoslav.eu
'
' Changelog:
' 2003.12, Initial version
' 2024.08, Improved program readability using AI

DECLARE SUB FillSegment (x1, y1, x2, y2, xx1, yy1, xx2, yy2)
DIM SHARED spiralX(1 TO 10000)
DIM SHARED spiralY(1 TO 10000)
DIM SHARED angles(1 TO 10000)
DIM SHARED phaseAngles(1 TO 10000)
DIM SHARED spiralLength
SCREEN 12
stepUnit = 200
spiralLength = 0

' Generate the spiral points
FOR angleIndex = 1 TO 97 STEP .15
    spiralLength = spiralLength + 1
    stepUnit = SIN(angleIndex / 31) * 100
    xPos = SIN(angleIndex) * stepUnit * 3 + 320
    yPos = COS(angleIndex) * stepUnit + 250
    yPos = yPos - (COS(angleIndex / 31) * 200)
    angles(spiralLength) = angleIndex
    phaseAngles(spiralLength) = angleIndex / 31
    spiralX(spiralLength) = xPos
    spiralY(spiralLength) = yPos
    PSET (xPos, yPos), 15
NEXT angleIndex

' Load texture data from file
OPEN "texture.dat" FOR INPUT AS #1
DIM SHARED textureData$(1 TO 1000)
textureIndex = 0
1
    LINE INPUT #1, textureLine$
    IF LEFT$(textureLine$, 3) = "END" THEN GOTO 2
    textureIndex = textureIndex + 1
    textureData$(textureIndex) = textureLine$
GOTO 1
2
CLS

' Apply texture to the spiral
textureIndex = 1
FOR charIndex = 1 TO 20
    FOR textCharIndex = 1 TO LEN(textureData$(charIndex))
        textureChar$ = RIGHT$(LEFT$(textureData$(charIndex), textCharIndex), 1)
        textureIndex = textureIndex + 1
        IF textureIndex > spiralLength - 43 THEN GOTO DONE
        teeVal = SIN(angles(textureIndex + 32)) - COS(phaseAngles(textureIndex))

        ' Draw lines if the condition is met
        IF teeVal <= 0 THEN
            LINE (spiralX(textureIndex), spiralY(textureIndex))-(spiralX(textureIndex + 1), spiralY(textureIndex + 1)), 15
            LINE (spiralX(textureIndex), spiralY(textureIndex))-(spiralX(textureIndex + 42), spiralY(textureIndex + 42)), 15
            ' Fill the segment if the character matches
            IF textureChar$ = "M" THEN
                CALL FillSegment(spiralX(textureIndex), spiralY(textureIndex), spiralX(textureIndex + 1), spiralY(textureIndex + 1), spiralX(textureIndex + 42), spiralY(textureIndex + 42), spiralX(textureIndex + 43), spiralY(textureIndex + 43))
            END IF
        END IF
    NEXT textCharIndex
NEXT charIndex
DONE:
a$ = INPUT$(1)
SYSTEM

' Subroutine to fill a segment with lines
SUB FillSegment (x1, y1, x2, y2, xx1, yy1, xx2, yy2)
    ' Assign input parameters to local variables
    xStart = x1
    yStart = y1
    xEnd = x2
    yEnd = y2
    xxStart = xx1
    yyStart = yy1
    xxEnd = xx2
    yyEnd = yy2

    ' Calculate step increments
    j = 10
    xStep = (xEnd - xStart) / j
    yStep = (yEnd - yStart) / j
    xxStep = (xxEnd - xxStart) / j
    yyStep = (yyEnd - yyStart) / j

    ' Draw lines between the points
    FOR a = 1 TO j
        xStart = xStart + xStep
        yStart = yStart + yStep
        xxStart = xxStart + xxStep
        yyStart = yyStart + yyStep
        LINE (xStart, yStart)-(xxStart, yyStart), 15
    NEXT a
END SUB

6. Textured and shaded spherical spiral

spiral, 6.png

Similar to previous spiral, Line segments are connected between the neighbors. Spiral height and width are calculated such that sphere is formed. Sphere is textured. Texture is loaded from file: texture1.dat . Invisible surface detection and removal is attempted. Sphere is shaded.

spiral, 6.bas

' Program to render fancy looking textured and shaded spiral. Texture is loaded from file.
' By Svjatoslav Agejenko.
' Email: svjatoslav@svjatoslav.eu
' Homepage: http://www.svjatoslav.eu
'
' Changelog:
' 2003.12, Initial version
' 2024.10, Improved program readability using AI

DECLARE SUB fill(x1, y1, x2, y2, xx1, yy1, xx2, yy2, hel)
DIM SHARED torux(1 TO 10000)
DIM SHARED toruy(1 TO 10000)
DIM SHARED sin1(1 TO 10000)
DIM SHARED cos1(1 TO 10000)
DIM SHARED tor

' Set the screen mode to 12
SCREEN 12
su = 200
tor = 0

' Calculate points for the spiral
FOR a = 1 TO 97 STEP .15
    tor = tor + 1
    su = SIN(a / 31) * 100
    x = SIN(a) * su * 3 + 320
    y = COS(a) * su + 250
    y = y - (COS(a / 31) * 200)
    sin1(tor) = a
    cos1(tor) = a / 31
    torux(tor) = x
    toruy(tor) = y
    ' Set the pixel at (x, y) to color 15
    PSET (x, y), 15
NEXT a

' Open the text file for input
OPEN "texture1.dat" FOR INPUT AS #1
DIM SHARED text$(1 TO 1000)

a = 0
1
' Read a line from the file
LINE INPUT #1, a$
' Check if the line is the end marker
IF LEFT$(a$, 3) = "END" THEN GOTO 2

' Increment the counter and store the line in the text array
a = a + 1
text$(a) = a$
GOTO 1
2
' Close the file
CLOSE #1

' Clear the screen
CLS
a = 1
' Loop through each character in the text
FOR c = 1 TO 20
    FOR b = 1 TO LEN(text$(c))
        ' Get the current character
        a$ = RIGHT$(LEFT$(text$(c), b), 1)

        ' Increment the counter
        a = a + 1
        ' Check if we have reached the end of the points array
        IF a > tor - 43 THEN GOTO 3

        ' Calculate the angle for the current point
        tee = SIN(sin1(a + 32))
        tee = tee - COS(cos1(a))

        ' Draw lines based on the calculated angle
        IF tee <= 0 THEN
            LINE (torux(a), toruy(a))-(torux(a + 1), toruy(a + 1)), 15
            LINE (torux(a), toruy(a))-(torux(a + 42), toruy(a + 42)), 15
            hel = 10
            hel1 = COS(cos1(a) - 1) + .5
            hel2 = SIN(sin1(a) + 1) + 1
            ' Adjust brightness based on the angles
            IF hel2 > 1 AND hel1 > 1 THEN
                hel3 = (hel2 - 1) * (hel1 - 1) * 8
                hel = hel / (hel3 + 1)
            END IF

            ' Adjust brightness if the character is "M"
            IF a$ = "M" THEN hel = hel / 3

            ' Fill the shape with the calculated brightness
            fill torux(a), toruy(a), torux(a + 1), toruy(a + 1), torux(a + 42), toruy(a + 42), torux(a + 43), toruy(a + 43), hel
        END IF
    NEXT b
NEXT c

' Wait for user input
3
a$ = INPUT$(1)
SYSTEM

SUB fill(zx1, zy1, zx2, zy2, zxx1, zyy1, zxx2, zyy2, hel)

' This subroutine fills a shape defined by four points with a specified brightness
' x1,y1  ----------------   xx1,yy1         hel - brightness
'        |              |
'        |              |
'        |              |
'  x2,y2 ----------------   xx2,yy2

' Assign local variables for clarity
x1 = zx1
y1 = zy1
x2 = zx2
y2 = zy2
xx1 = zxx1
yy1 = zyy1
xx2 = zxx2
yy2 = zyy2

' Calculate the differences and distances between points
j1 = x1 - x2
j2 = y1 - y2
j3 = SQR((j1 * j1) + (j2 * j2))

j4 = xx1 - xx2
j5 = yy1 - yy2
j6 = SQR((j4 * j4) + (j5 * j5))

' Calculate the average distance and adjust for brightness
j7 = (j3 + j6) / 2
j = j7 / hel

' Calculate the step sizes for each axis
x3 = (x2 - x1) / j
y3 = (y2 - y1) / j
xx3 = (xx2 - xx1) / j
yy3 = (yy2 - yy1) / j

' Draw lines between the points with the specified brightness
FOR a = 1 TO j
    x1 = x1 + x3
    y1 = y1 + y3
    xx1 = xx1 + xx3
    yy1 = yy1 + yy3
    LINE (x1, y1)-(xx1, yy1), 15
NEXT a
END SUB